向量索引

高效率地从高维向量中, 做相似性查找, 是个让人头疼的问题, 但这又有非常多的应用场景, 比如相似推荐, 以图搜索等. 解决这个问题的方法也有很多, 比如 annoy, hnsw 等等. 京东开源的 vearch, Apache 开源的 Milvus.

HNSW 算法理论

Hierarchcal Navigable Small World graphs, 常用有三个实现

• nmslib, Non-Metric Space Library, An efficient similarity search library and a toolkit for evaluation of k-NN methods for generic non-metric spaces.
• hnswlib, Header-only C++/python library for fast approximate nearest neighbors
• faiss, A library for efficient similarity search and clustering of dense vectors.

从 ann-benchmarks 来看, numslib 实现效果最佳.

朴素想法

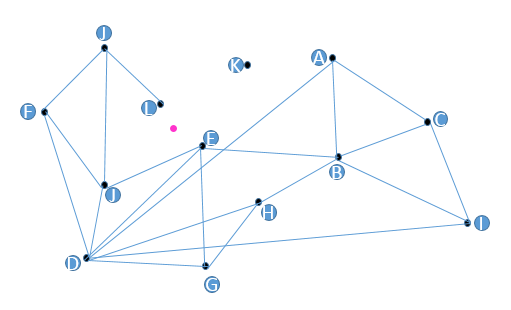
假设我们现在有 13 个 2 维数据向量，我们把这些向量放在了一个平面直角坐标系内，隐去坐标系刻度，它们的位置关系如上图所示。

朴素查找法: 把某些点之间连上线, 构成一个查找图, 有连接关系的点称为 “友点”. 当我们想查找与粉色点最近的点时, 我们从任意黑色点出发, 计算它以及所有友点, 与粉色点的距离, 从中选出离粉色点最近的一个点, 作为下一个出发点, 继续前面的步骤. 如果当前黑色点比它所有的友点都近, 那么终止查找, 这个黑色点就是距离粉色点最近的点.

• 假设从 C 点出发, 计算 (C,A,B,I) 与粉色点的距离, B 最近
• 从 B 点出发, 计算 (B,E,H) 与粉色点的距离 (遍历过的节点跳过), E 最近
• 从 E 点出发, 计算 (E,J,D,G) 与粉色点的距离, E 最近, 终止查找

就这个场景而已, 最近的应该是 L, 我们一起来看看朴素想法有哪些缺陷:

• K 点无法被查询到
• 假设我们要查找最近的两个点, 但这两个点之间又没有连线, 那么会大大影响效率
• D 点真的需要这么多友点吗? 如何确定谁和谁是友点

解决方案也很简单, 在构图时

• 所有数据向量节点都必须有友点
• 所有距离相近 (相似) 到一定程度的向量必须互为友点
• 尽量减少每个节点的 “友点” 数量

在图论中, 正好有个算法专门解决上述缺陷 — 德劳内 (Delaunay) 三角剖分算法. 这个算法可以达成如下要求: 1，图中每个点都有“友点”。2，相近的点都互为“友点”。3，图中所有连接（线段）的数量最少。效果如下图。

实际上, HNSW 并未采用德劳内三角剖分法来构建查找图, 因为时间复杂度太高, 此外, 查找效率不够高, 如果初始点与临近点距离很远的话, 我们需要多次跳转才能到达, 需要“高速公路”机制.

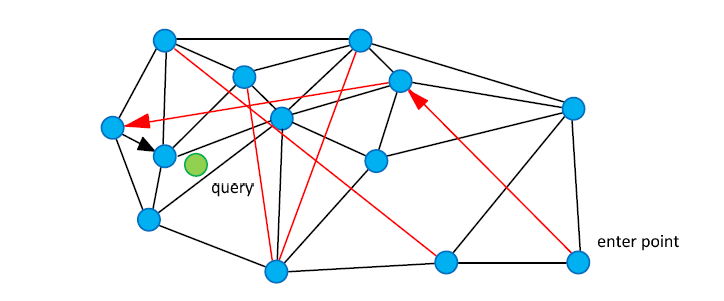
NSW 构图法

随机逐个插入节点, 当插入节点时, (按前面的朴素想法) 找到与图中最近的 m 个节点, 连上边即可.

构图算法是逐点随机插入的，这就意味着在图构建的早期，很有可能构建出“高速公路”。

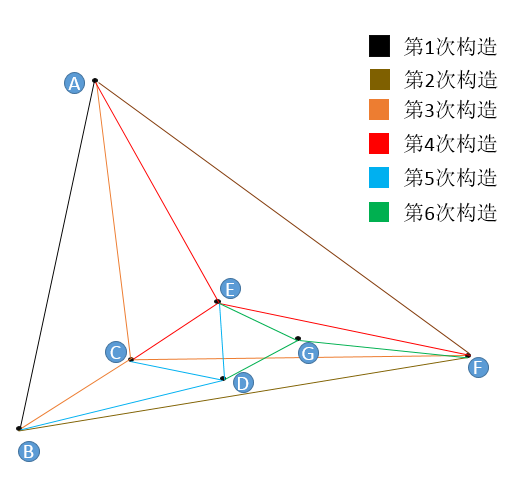
我们对 7 个二维点进行构图，用户设置 $m=3$。

• 首先初始点是 A 点（随机出来的），A 点插入图中只有它自己，所以无法挑选“友点”。
• 然后是 B 点，B 点只有 A 点可选，所以连接 BA，此为第 1 次构造。
• 然后插入 F 点，F 只有 A 和 B 可以选，所以连接 FA，FB，此为第 2 此构造。
• 然后插入了 C 点，同样地，C 点只有 A，B，F 可选，连接 CA，CB，CF，此为第 3 次构造。
• 重点来了，然后插入了 E 点，E 点在 A，B，F，C 中只能选择 3 个点作为“友点”，根据我们前面讲规则，要选最近的三个，怎么确定最近呢？朴素查找！由此，我们找到了 E 的三个近点，连接 EA，EC，EF，此为第四次构造。
• 第 5 次构造和第 6 次与 E 点的插入一模一样，都是在“现成”的图中查找到 3 个最近的节点作为“友点”，并做连接。

HNSW 就是 NSW 再优化版本, 改天继续看

nmslib 版 hnsw 性能调研

测评方案：

1. 测试版本为 nmslib1.6
2. 按照业务场景，随机构造 100 维的 30 万篇笔记，随机选择 query 获取 10 篇最近邻笔记
3. hnsw 在索引构建环节有 3 个重要可调参数 (M，efConstruction，post 默认为 2), 测评中选择距离度量方式为 l2; 在 query 环节有 1 个可调参数（efSearch）。官网参数调优说明，参数调优
4. 测试机器为 rec-dev01h，索引构建默认会按照核数并发，query 只使用单线程
5. 衡量指标：
   1. 构建时间
   2. 内存占用
   3. query时间
   4. recall

方案选择逻辑：

1. 对不同参数下的结果按照 recall 进行排序
2. 分别算出 query_time, memory, index_time 在整体中的排名，综合成本使用 query_time 排名 + index_time 排名
3. 先选定预期的 recall，如 0.99，选择符合 recall 需求的综合成本最低的方案，本次测试中 recall 0.99 的最佳方案如下图，单次 query 耗时 6.43ms，构建时间为 310s

实际测试数据：

数据分析:

参考资料

• 高维向量索引库-Nmslib性能调研@胡一刀
• approximate nearest neighbor (ANN) benchmarks
• 一文看懂HNSW算法理论的来龙去脉